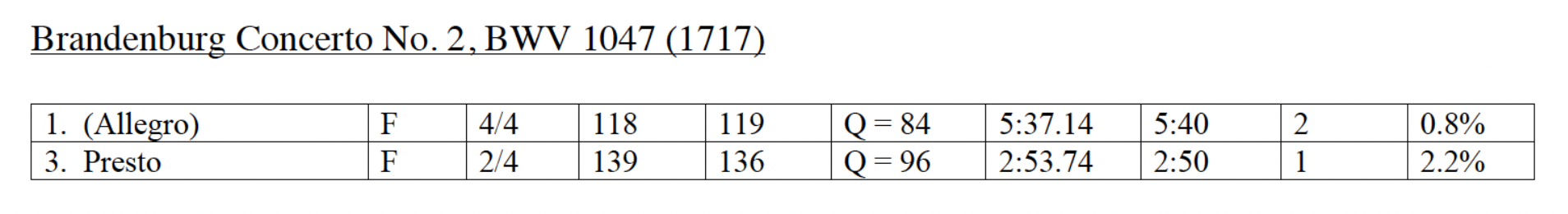Chapter 6: Bach, Musical Architect & the Divine Numbers 1-2-3
“Music is liquid architecture; Architecture is frozen music.” – Johann Wolfgang van Goethe
Bach, Musical Architect & Theologian
In Chapter 5, the forty examples of extremely accurate duration ratios (with an average discrepancy of 1.2%) from a wide variety of works and genres indicates that Bach operated with a unique system that allowed him to achieve these ratios. Skeptics may be inclined to relegate these findings to sheer coincidence; however, if all the breathtakingly accurate duration ratios demonstrated in Chapter 5 are coincidental, then why isn’t unity and order in architecture also relegated to sheer coincidence? For example, if an architect designs a house that contains two adjacent rooms of equal dimensions, the chances of this being coincidental are zero. After all, one does not need a Ph.D. in mathematics to know that the architect who planned the size of the two rooms intended them to be equal in size. Likewise, if one room is two times or one-half times larger than the other room, everyone knows that a human being, an architect, planned the rooms to have these specific related dimensions.
The orderly and related dimensions of rooms in houses and buildings simply do not happen by themselves. Seen in this light, it is not “radical” or “controversial” at all to suggest that the most mathematically-minded composer in the history of music, self-professed “musical scientist,” and “Isaac Newton of music” would plan his movements to share duration ratios. “Size” or “dimension” in architecture is analogous to “duration” or “time” in music. An architect may plan a room to be 5 square meters, while Bach may have planned a movement to last 5 minutes. An architect may plan one room to be 7 square meters and another related room to be 4 and 1/3 square meters to achieve a 3:2 dimension ratio, while Bach may have planned one movement to last 7 minutes and a related movement to last 4:40 to achieve a 3:2 duration ratio (Diagram 1).
Bach’s cantatas (or perhaps a selection of them) are analyzed in Part 2 and the easiest way to describe the duration ratios present in them is through the architecture analogy. Virtually all the major movements of Bach’s cantatas have multiple accurate duration ratios, not including the minor movements of recitatives and chorales. Bach’s typical cantata consists of one or more choruses (SATB), one or more solo or duet arias, one or more chorales, one or more recitatives. Hence, a Bach cantata can be likened to a house where the rooms are the major movements, which always share accurate duration ratios, and the hallways or pathways are the minor movements, which may or may not share accurate duration ratios. For example, let us construct a hypothetical cantata consisting of two choruses, two arias, two recitatives, and one chorale. The choruses and arias are the rooms of the house, while the two recitatives and chorale are the pathways between the rooms. In this hypothetical seven-movement cantata, the two choruses are the first and last of the major movements, the first and sixth movements, the arias are the second and fourth movements which lie between these outer pillars, the recitatives lie between the first chorus and two arias, and the chorale is the seventh and final movement.
Regarding the durations of the movements, this cantata has the choruses each lasting 5:00 while the first aria has a duration one-third shorter, 3:20, and the second aria has a duration one-half shorter, 2:30. This makes a total of three duration ratios, which are three different combinations of 1-2-3. The first and third movements (Chorus-Aria) relate 3:2, the fifth and sixth movements (Aria-Chorus) relate 1:2, and the first and sixth movements (Chorus-Chorus) relate 1:1. Typical Bach recitatives last between one and two minutes while a typical chorale lasts around one minute. All these durations total 20 minutes. Thus, if Bach desired a twenty-minute cantata for a church service, he apparently (according to all the evidence in Part 2) mapped out the plan either on paper (which could be expensive) or in his head (which was free) like the plan given here. If Bach desired a thirty-minute cantata or perhaps a forty-five-minute cantata for a grand occasion, he simply increased the durations of the movements and/or added more movements (Table 1).
Recognizing whole number durations (like 3:00, 4:00, 5:00, 6:00) and multiple duration ratios in Bach’s church cantatas and masses, as well as all his organ compositions, explains and illuminates Bach’s famous quote about creating “a well-regulated” church music. Traditionally, this quote (which is frequently cited by scholars) is thought to refer to Bach’s system of harmony, counterpoint, and other compositional techniques; however, it makes more sense that Bach was referring to his system of controlling or regulating the formal dimensions and architectural components of his works. Being blessed with the ability to compose large-scale, multi-movement works of any desired length consisting of movements that share multiple duration ratios (by means, no easy feat) accurately explains this quote:
Analysis of most of Bach’s major works in all genres in Chapter 5 and all of Part 2 indicates that Bach’s system of tempo was one of large-scale architecture in which most if not all the duration ratios between movements consist of a variety of possible combinations using the numbers 1-2-3. This is musical architecture at its simplest and most economical. In Chapter 4 it is shown that Bach had a fascination and preoccupation with symmetry mainly to symbolize theologically The Alpha & The Omega. Continuing the theological symbolism, combining 1-2-3 in any order symbolizes the complete three-part Godhead, The Father, The Son, The Holy Spirit, known as The Holy Trinity. The number 1 represents God, the Father, the number 2 represents the two natures of Christ, human and divine, while the number 3 represents the Holy Spirit, which equals the sum of 1 and 2. By achieving durations that relate 1:1, 1:2 (2:1), 2:3 (3:2), Bach imbued his music symbolically with all possible combinations of The Holy Trinity. Such all-encompassing theological symbolism is corroborated by Bach’s own words:
Bach was a “scientist of music” and “theologian of music” who already early in his career as a composer (as early as his early 20s) strove to give glory to God by pairing or grouping movements using all possible combinations of the numbers 1-2-3 to achieve duration ratios (Diagram 2).
Bach’s Standard Operating Procedure (Modus operandus)
Study of the actual and ideal durations from the forty examples discussed in Chapter 5 as well as the analysis of works in Part 2 leads to the observation that most of the duration ratios other than 1:1 consist of one longer movement of “whole-number duration” such as six or eight minutes, 6:00 or 8:00, and another shorter movement either one-half shorter, 3:00 or 4:00, or one-third shorter, 2:40 or 5:20. This is the basis behind the hypothetical cantata discussed earlier. Bach’s entire system of tempo was founded upon this principle of creating duration pairs and duration groups of two or more movements. Thus, it is helpful to summarize Bach’s most common durations and duration ratios with four tables that include virtually every possible combination for every quarter of a minute, or fifteen seconds (Tables 2-5).
Study of the duration ratios and tempo ratios from Chapter 5 shows that Bach usually avoided pairing movements of the same meter and tempo as this can become monotonous and boring. Instead, Bach usually planned two such movements to have faster and slower tempos to varying degrees and imbued upon them diverse rhythmic characteristics by his choice of time signature combined with various rhythmic motifs that suggest a particular dance or other styles. If two movements are paired that share the same meter, then one is always slower or faster than the other to facilitate a particular duration ratio. Bach’s norm was clearly one of a subtle but noticeable change in tempo from one movement to the other except in the case of a dramatic 1:2 or 2:1 shift in tempo, which occurs not infrequently.
For example, Chapter 5 shows a total of seven examples of paired movements of the same meter (in the spreadsheets below). Except for the two examples of a 2:1 (96:48) and 1:2 (48:96) tempo ratio, all other instances show two tempos on neighboring rows from the tempo matrix. In other words, Bach preferred one movement “a little faster” and the other movement “a little slower” where “a little” simply means one step up or down on the natural tempo progression: 42-48-54-63-72. The five examples where one movement is a little slower or faster consist, surprisingly, of five different tempo pairings: 42:48, 54:63, 63:54, 72:63, 63:72. This indicates that Bach strove for great variance and diversity in the pairing of tempos. Slight differences in tempo in duration pairs such as these are usually innately felt by most experienced performers. For example, most organists naturally choose a slightly faster tempo (or sometimes “much” faster, which of course is incorrect) for the Fugue than the Passacaglia (BWV 582). Likewise, most pianists naturally choose a slightly slower tempo for the D-sharp minor Fugue than the Prelude (BWV 877). Hence, Bach’s pairing of one tempo slightly slower or faster than the other tempo is by no means radical or iconoclastic as Bach simply chose the most natural tempo for each movement.
Chapter 5 shows a total of eleven tempos: 42, 48, 54, 56, 63, 64, 72, 84, 96, 108, 126. This is a highly practical tempo system since all possible combinations of two tempos reduce to a simple whole number ratio, which makes it easy to establish proportionally related ratios for the number of beats and/or number of measures. A complete gamut of simple whole number ratios is impossible assuming any other set of tempos, which is one of the main advantages of limiting the tempos exclusively to the tempos in the mathematically ideal tempo matrix.
Chapter 5 shows no fewer than 31 tempo pairings taken from 11 possible tempos, which reduce to seventeen simple whole number ratios that facilitate a total of five duration ratios: 1:1, 1:2, 2:1, 2:3, 3:2. The tempo ratios and pairings can be summarized in one spreadsheet (Table 6). Similarly, Chapter 5 also shows no fewer than 18 beat pairings, which can also be summarized in one spreadsheet (Table 7).
Study of the tempo and beat ratios in Tables 6-7 shows the same ratios for tempos and beats, which always reduce to a complete gamut of simple whole number ratios. Thus, combining Tables 6 and 7 and adding additional possible ratios, a master spreadsheet can be created that lists virtually every possible simple whole number ratio ascending in value from 1:3 to 3:1. The tempo ratios and tempo pairings for virtually Bach’s complete works can be summarized in this single spreadsheet, which consists exclusively of thirteen tempos (36, 42, 48, 54, 56, 63, 64, 72, 84, 96, 108, 126, 128) that total no fewer than 27 tempo ratios and 55 tempo pairings. This shows that Bach had virtually endless possibilities of diversifying his tempos and tempo ratios to achieve only a handful of duration ratios (Table 8).
Speed-Distance-Time = Tempo-Beats-Duration
Study of Chapter 5 and the analysis of works in Part 2 shows that Bach’s entire system of tempo and duration was founded upon and dependent upon the presence of simple whole number ratios between tempos and beats to facilitate primarily five duration ratios – 1:1, 1:2, 2:1, 2:3, 3:2 – and occasionally, 1:3 and 3:1. The most reliable, consistent, and least expensive method (actually, free!) of calculating tempo, beats, or duration is the age-old formula for Speed-Distance-Time and its derivatives, which applied to musical composition and performance becomes Tempo-Beats-Duration. It is not known whether Bach used decimals or fractions in his calculations, but these three Tempo-Beats-Duration equations are easy and user-friendly, ensuring reliable and accurate calculations using exclusively fractions reduced to simple whole number ratios. Study of the durations and duration ratios in Bach’s music suggests that Bach was so skilled at these basic arithmetic calculations that he could most likely perform most of them in his head in only a few seconds’ time. Nothing less would be expected of the “Isaac Newton of Music.”
A popular notion among the masses is that the great composers wrote music effortlessly without consciously planning and the appropriate tempos were planned last as an afterthought. For example, the famous scene from the movie Amadeus of Mozart whimsically composing a work while playing billiards exemplifies and reinforces this popular notion. This is not rooted in reality. Contrary to what the masses are led to believe, it is impossible to compose a movement without first deciding upon at least three “fixed” elements determined from the outset, which are key, meter/style, and tempo. Keys and key signatures do not happen by themselves, but they need to be consciously decided upon before putting pen to paper. Likewise, meters (time signatures) and stylistic characteristics associated with the meters do not happen by themselves, but they also need to be decided upon before putting pen to paper.
The same applies to tempo. For example, before writing the first note for any of the Brandenburg Concertos, Bach decided on the tempo for each movement. Bach did not compose a movement and then decide on the tempo last but decided on his tempo first even before taking out his pen and dipping it in the inkwell. This mode of operation does not necessarily apply to movements to which Bach supplied tempo words (i.e., Allegro, Andante, etc.), like in the Brandenburg Concertos, but to all his works. For example, when composing a prelude and fugue for organ or keyboard that does not contain a tempo word (which includes most preludes and fugues), Bach decided on the tempo and character of each movement first, then composed the movements last. The popular belief among many performers that Bach did not supply tempo words for his preludes and fugues because he was unsure what tempos he wanted is ludicrous.
In musical composition, the only element that cannot be 100% fixed from the outset is measures. That is, Bach could have planned a certain number of measures for a movement not yet composed, like 240 measures for the third movement of Brandenburg Concerto No. 4 to achieve a duration of five minutes, yet it was not until reaching the final bar with his pen that the number of measures became cast into stone, in this case, 244 measures, four more than the original plan. (Please refer to the discussion of Brandenburg Concerto No. 4 in Chapter 5.) Hence, before putting pen to paper Bach decided upon the key, meter/style, and tempo – the “fixed” elements – which allowed determination of the “variable” element or number of measures. Musical analysis confirms that Bach’s usual or default tempos were 36, 42, 48, 54, 56, 63, 64, 72, 84, 96, 108, 126, which covers an extremely wide range of tempos.
To have an idea of what steps are required for Bach to have achieved a stunning number of extremely accurate duration ratios, seven examples have been chosen from the duration pairs discussed in Chapter 5. Let us reason through each pair and pretend that we are Bach. Please take time to fully understand each spreadsheet and how the two movements relate. Then, we will go through all the numbered steps required as if we were the composer.
Calculating 1:1 Duration Ratios
Steps required to achieve equal durations of three minutes
Determine the duration ratio – The two arias shall be equal in length at three minutes.
Determine the meters and tempos – The first aria, for tenor, shall be in 3/4 and have a fast Allegro/Vivace-style tempo of 96 bpm (in the “fours” column of the matrix). The second aria, for alto, shall be in 9/8 and have a slow pastorale-style tempo of 64 bpm (in the “threes” column of the matrix). The tempo ratio, 96:64, reduces to 3:2.
Determine the measures – To achieve three minutes for the tenor aria at its meter and tempo, it shall consist of 96 measures. To achieve three minutes for the alto aria at its meter and tempo, it shall consist of 64 measures. The measure ratio, 96:64, reduces to 3:2.
Compose the movements aiming for 96 and 64 measures – Bach composed 94 and 64 measures, achieving his goal with a mere two-measure (four seconds) discrepancy.
Steps required used to achieve equal durations of four minutes
Determine the duration ratio – The two arias shall be equal in length at four minutes.
Determine the meters and tempos – The first aria, for bass, shall be in 4/4 and have a moderately slow tempo of 54 bpm. The second aria, a duet for alto and bass, shall be in 3/4 and have a courante or minuet-style tempo of 108 bpm. The tempo ratio, 54:108, reduces to 1:2.
Determine the measures – To achieve four minutes for the bass aria at its meter and tempo, it shall consist of 54 measures. To achieve four minutes for the duet aria at its meter and tempo, it shall consist of 144 measures. The measure ratio 54:144 reduces to 3:8.
Compose the movements aiming for 54 and 144 measures – Bach composed 55 and 148 measures, achieving his goal within a mere 2.4% (1.4 seconds) average discrepancy. This results in two durations of just over four minutes.
Steps required to achieve equal durations of about 4:20
Determine the duration ratio – The first and fifth movements, the outer movements, shall be equal in length.
Determine the meters and tempos – The first movement shall be in 4/4 and have the usual or default Allegro of 84 bpm. The fifth movement shall be in 6/8 and have an Allegro of 56 bpm (in the “sixes” column of the matrix), making the two movements equal by fastest common note value (the sixteenth-note at 336 bpm). The tempo ratio, 84:56, reduces to 3:2.
Determine the measures for the first movement – There appears to be no measure goal here, which usually applies only to whole number durations like three or four minutes (like in the two examples above). However, to achieve a substantial duration of at least four minutes, the first movement shall consist of at least 84 measures.
Compose the first movement – Bach composed 91 measures, which consists of a total of 364 beats (91 x 4). Calculate its duration by setting up an equation and solving for “Duration” —> Duration = Beats ÷ Tempo —> Duration = 364 ÷ 84 = 4.33 (expressed as a fraction, 13/3) or four and one-third minutes, 4:20. Therefore, the fifth movement shall also last 4:20.
Determine the measures for the fifth movement – Set up an equation and solve for “Beats” —> Beats = Tempo x Duration —> Beats = 56 x 4.33 —> Beats = 242 (rounded off). Since the fifth movement shall consist of 242 beats and there are two beats per measure (in 6/8), then it shall consist of 121 measures to make its duration equal to that of the first movement.
Compose the fifth movement – Bach composed 119 measures, achieving his goal of 121 measures within a mere 0.8% (0.5 seconds) average discrepancy. Being that the actual measure ratio, 91:119, can be slightly adjusted to 90:120, which reduces to a 3:4 measure ratio, it is possible that Bach initially planned this measure ratio from the outset.
Calculating 1:2 and 2:1 Duration Ratios
Steps required to achieve a 1:2 duration ratio
Determine the duration ratio – The third movement shall be twice the duration of the second movement (without repeats), creating a 1:2 duration ratio, or equal in duration (with repeats).
Determine the meters and tempos – The second movement shall be in 4/4 with a relaxed Andante-style tempo of 63 bpm. The third movement shall be in 3/8 with a slow tempo of 72 bpm (in the “threes” column of the matrix). Although the beat of the third movement is a little faster than the beat of the second movement, the fastest common note value (the sixteenth and triplet sixteenth) decelerates slightly (from 252 to 216 bpm), making the third movement slower than the second movement. The tempo ratio, 63:72, reduces to 7:8.
Determine the measures – Set up an equation and solve for “Beats” —> Beats = Tempo x Duration —> Beats = 7/8 x 1/2 = 7/16, meaning the beat ratio between movements shall be 7:16 to achieve a 1:2 duration ratio at the chosen tempos. The beat ratio of 7:16 is one-half of the tempo ratio, 7:8. Only two possibilities exist for numbers in the matrix that relate 7:16, 42:96 and 84:192, in which the latter is chosen. Therefore, the second movement shall consist of 84 beats, or 21 measures, while the third movement shall consist of 192 beats, or 64 measures.
Compose the movements aiming for 21 and 64 measures – Bach composed 22 and 64 measures, achieving his goal with a mere one-measure (three seconds) discrepancy, achieving a 1:2 duration ratio of 1:20-2:40.
Steps required to achieve a 2:1 duration ratio
Determine the duration ratio – The third movement shall be half the duration of the first movement, creating a 2:1 duration ratio between the outer movements.
Determine the meters and tempos – The first movement shall be in 4/4 with the usual default Allegro of 84 bpm. The third movement shall be in 2/4 and have a faster Presto-style tempo of 96 bpm. The tempo ratio, 84:96, reduces to 7:8.
Determine the measures – Knowing the meters, tempos, and duration ratio of the two movements allows the establishment of an equation solving for “Beats” —> Beats = Tempo x Duration —> Beats = 7/8 x 2/1 = 7/4, meaning the beat ratio between movements shall be 7:4 to achieve a 2:1 duration ratio at the chosen tempos. The beat ratio of 7:4 is two times the tempo ratio, 7:8. Since the first movement has twice as many beats per measure as the third movement and the ratio of beats is 7:4, then the ratio of measures becomes 7/4 x 1/2 = 7/8. In other words, the measures for the two movements shall relate 7:8 to facilitate a 2:1 duration ratio at the chosen tempos.
Compose the first movement – Bach composed 118 measures for the first movement.
Determine the measures for the third movement – Since the first movement has 118 measures, then the third movement shall have 118 x 8/7 = 135 measures (rounded off).
Compose the third movement aiming for 135 measures – Bach composed 139 measures achieving his goal with a mere four-measure (1.3 seconds) discrepancy, achieving a 2:1 duration ratio of 5:40-2:50 (rounded off).
Calculating 2:3 and 3:2 Duration Ratios
Steps required to achieve a 2:3 duration ratio
Determine the durations and duration ratio – The fugue shall last seven minutes and the toccata shall last one-third shorter, or 4:40, creating a 2:3 duration ratio of 4:40-7:00.
Determine the meters and tempos – The toccata shall be in 4/4 with the usual default Allegro of 84 bpm. The fugue shall be in 2/2 and have a more moderate tempo of 63 bpm. The tempo ratio, 84:63, reduces to 4:3.
Determine the measures – For the fugue, set up an equation and solve for “Beats” —> Beats = Tempo x Duration —> Beats = 63 x 7 = 441 —> Measures = 441 ÷ 2 = 221 (rounded off). In other words, the fugue shall consist of 221 measures to facilitate a duration of seven minutes at the chosen tempo of 63 bpm. For the toccata, set up and equation and solve for “Beats” —> Beats = Tempo x Duration —> Beats = 84 x 4.66 = 391 (rounded off) —> Measures = 391 ÷ 4 = 98 (rounded off). In other words, the toccata shall consist of 98 measures to facilitate a duration of 4:40 at the chosen tempo of 84 bpm.
Compose the movements aiming for 98 and 221 measures – Bach achieved one more measure for each, 99 and 222, showing a virtually precise 2:3 duration ratio of 4:40-7:00.
Steps required to achieve a 3:2 duration ratio
Determine the durations and duration ratio – The passacaglia shall last eight minutes and the fugue shall last one-third shorter, or 5:20, creating a 3:2 duration ratio of 8:00-5:20.
Determine the meters and tempos – The passacaglia shall be in 3/4 with a moderate tempo of 63 bpm. The fugue shall also be in 3/4 with a slightly faster tempo of 72 bpm. The tempo ratio, 63:72, reduces to 7:8.
Determine the measures – For the passacaglia, set up an equation and solve for “Beats” —> Beats = Tempo x Duration —> Beats = 63 x 8 = 504 —> Measures = 504 ÷ 3 = 168. In other words, the passacaglia shall consist of 168 measures to facilitate a duration of eight minutes at the chosen tempo of 63 bpm. For the fugue, set up an equation and solve for “Beats” —> Beats = Tempo x Duration —> Beats = 72 x 5.33 = 384 (rounded off) —> Measures = 384 ÷ 3 = 128. In other words, the fugue shall consist of 128 measures to facilitate a duration of 5:20 at the chosen tempo of 72 bpm.
Compose the movements aiming for 168 and 128 measures – Bach achieved 168 measures for the passacaglia and 124 measures for the fugue, showing that Bach hit the target measures for the passacaglia precisely but fell four measures short of the 128-measure ideal in the fugue, which amounts to ten seconds. This provides a plausible explanation for Bach’s addition of “Adagio” in the penultimate measure. That is, falling short of his ideal in the fugue by four measures (or 3.1% discrepancy, which for Bach was a greater than average margin of error), Bach simply added “Adagio” in the penultimate measure to extend its duration by a few seconds to come as close as possible to a 3:2 duration ratio of 8:00-5:20.
Prelude and Fugue in E-flat Major for Organ
To conclude, let us now subject this system of tempo and duration to the ultimate test. Let us revisit the great organ Prelude and Fugue in E-flat Major, BWV 552, that forms the bookends or The Alpha & The Omega (see Chapter 4) to Clavierübung III. It has already been established in Chapter 4 that it can be assumed Bach planned the opening and closing movements of this great opus to be equal in duration. For sake of the test, let us pretend once again that we are Bach and that we have planned the two movements to have equal durations. Let us go through all the steps required to complete such an ambitious task. If you possess a score of BWV 552, please consult it when reading through the steps listed below. Please refrain from looking at the spreadsheet either before or during the reading of the text. Reading and understanding all the steps will help interpreting the spreadsheet printed at the end of this chapter.
Steps to achieve equal durations in BWV 552
Determine the durations and duration ratio – For this grand prelude and fugue, let us make each seven and a half minutes, 7:30, which totals a nice and even 15 minutes.
Choose a meter, style, and tempo for the prelude – The prelude shall be an energetic and virtuosic Allegro but with a rather slow half-note beat of 54 bpm as indicated by the cut-time meter.
Determine the measures for the prelude – Set up an equation and solve for “Beats” —> Beats = Tempo x Duration —> Beats = 54 x 7.5 = 405 —> Measures = 405 ÷ 2 = 203 (rounded off). In other words, the prelude shall consist of 203 measures to last 7:30 at the chosen tempo of 54 bpm.
Compose the prelude aiming for 203 measures – Bach achieved a total of 205 measures, showing that he exceeded his goal by only two measures making its duration a mere five seconds longer than the ideal, 7:35.
Plan the architecture of the fugue – The fugue shall consist of three sections that total 7:30. The most logical way to do this is to plan each section to increase gradually in duration. For example, the duration progression 2:00-2:30-3:00 naturally adds to 7:30, which is the most straightforward and logical way to arrange these blocks of time.
Choose a meter, style, and tempo for each section of the fugue – The first section shall be in 4/2 at a moderate tempo of 72 bpm. The second section shall have the tempo and character of a 6/4 courante, whose natural tempo is 108 bpm. (Kirnberger specifically describes 6/4 as a slow meter, which disproves the fast tempo for this section played by virtually all organists.) The third section shall be in 12/8 with a tempo of 48 bpm (or 144 bpm per eighth). This shows a noticeable acceleration from the second section in that the quarter-note speed of 108 bpm accelerates by one-third to 144 bpm. (Most organists make almost no distinction in tempos between the 6/4 and 12/8 in this fugue and play both sections too fast.) Notice that the three tempos chosen for the fugue, 72:108:144, reduce to 2:3:4, which corresponds to the gradually increasing durations of the three sections, 2:00-2:30-3:00.
Determine the measures for each section of the fugue – For the first section, set up an equation and solve for “Beats” —> Beats = Tempo x Duration —> Beats = 72 x 2 = 144 —> Measures = 144 ÷ 4 = 36. For the second section, Beats = 108 x 2.5 = 270 —> Measures = 270 ÷ 6 = 45. For the third section, Beats = 48 x 3 = 144 —> Measures = 144 ÷ 4 = 36. These equations indicate that the three sections of the fugue shall consist of a symmetrical number of measures, 36:45:36, which reduces to 4:5:4., to achieve the durations 2:00-2:30-3:00 at their chosen tempos.
Compose the fugue aiming for 36:45:36 measures – Bach achieved these measures precisely, resulting in a duration of precisely 7:30 as planned!
